庵智幸 情報学研究科博士課程学生、大塚敏之 同教授の研究グループは、多項式で表されるような制約付き非線形最適化問題に対し、その全ての最適解が満たすような条件式を導出するアルゴリズムの開発に成功しました。
実社会におけるあらゆる問題は、守らなければならない制約条件のもとで、何らかの評価指標を最小化あるいは最大化する制約付き最適化問題として定式化することができます。この制約付き最適化問題を解く際に、最適解が満たすべき条件である最適性必要条件が重要になります。既に様々な最適性必要条件が提案・研究されていますが、中でもKarush-Kuhn-Tucker(KKT)条件は、方程式で記述できるため具体的な最適解を計算するのに適しており、多くの理論的あるいは応用的な研究成果の基礎となっています。しかし、一部の最適解に対してはKKT条件が最適性必要条件にならないこと、つまり、KKT条件を解いても一部の最適解を見つけられないことが知られていました。
本研究では、制約条件を破ることに対してペナルティを課すという古典的な解法に、多項式を数式のまま計算機で厳密に処理できる数式処理という、比較的新しい技術を組み合わせることで、全ての最適解が満たす条件式を導出しました。明確に方程式として書き表すことのできる最適性必要条件としては、1951年にKKT条件が発表されて以来、およそ70年ぶりの成果と考えられます。この条件式は計算機で具体的な最適解を求めるのに利用できるため、従来のKKT条件では見つけられなかった新しい最適解の発見や、この条件式を基礎とする新たな最適化アルゴリズムの開発に繋がります。
本研究成果は、2020年10月31日に、国際学術誌「Journal of Operations Research Society of Japan」のオンライン版に掲載されました。
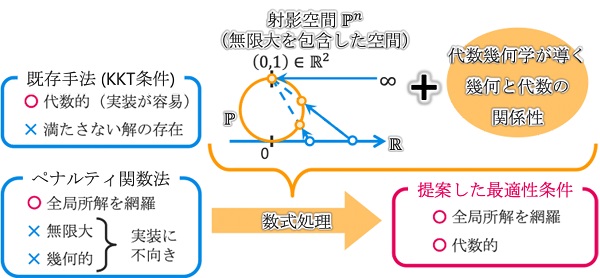
図:本研究の概要図
詳しい研究内容について
書誌情報
【DOI】 https://doi.org/10.15807/jorsj.63.114
【KURENAIアクセスURL】 http://hdl.handle.net/2433/255892
Tomoyuki Iori, Toshiyuki Ohtsuka (2020). LIMIT OPERATION IN PROJECTIVE SPACE FOR CONSTRUCTING NECESSARY OPTIMALITY CONDITION OF POLYNOMIAL OPTIMIZATION PROBLEM. Journal of the Operations Research Society of Japan, 63(4), 114-133.





