ターゲット
公開日
臨界点は、宇宙から素粒子まで様々なスケールの相転移現象に現れる普遍的な概念です。臨界点近傍では、系のミクロな性質によらないスケーリング則や臨界指数が現れることが知られており、これらの現象は統計物理学をはじめとした物理学全体を貫く研究対象として幅広く研究されてきました。
和田辰也 基礎物理学研究所博士課程学生、北澤正清 同講師らの研究グループは、様々な系の相図上に現れる臨界点の位置を求めるための新しい一般的な手法を開発しました。この手法は、複素パラメーター空間における分配関数のゼロ点であるリーヤンゼロの比を使うという画期的なアイデアに基づいており、臨界点の位置などの情報を系統的な手順で決定することができます。また、この手法を3次元3状態Potts模型の数値計算に適用して、その有効性を確認しました。この手法の適用範囲は系の詳細には依存しないため、物性物理学のみならず、有限温度有限密度QCDの相図に存在が予想される臨界点の位置決定など、幅広い系の臨界現象への適用が期待されます。
本研究成果は、2025年4月24日に、国際学術誌「Physical Review Letters」にオンライン掲載されました。さらに本論文は、同誌の「Editors' Suggestion」(注目論文)に選定されました。
研究者のコメント
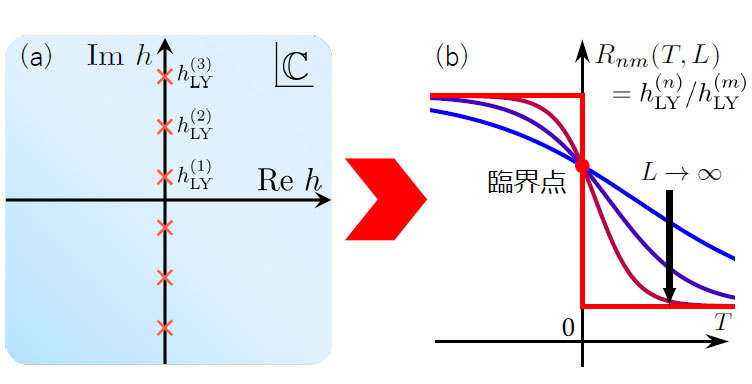
「リーヤンゼロを用いたQCD臨界点の探索は近年注目を受けている研究です。しかし、先行研究では有限体積であることを無視しており、私たちのグループでは、この解析は臨界点の位置を大きく変化させうるという点で深刻な問題であると考えていました。有限体積のリーヤンゼロの比というシンプルな量から臨界点を特定することが可能であると示せました。今後当初の目的であったQCDだけでなく、様々な理論へ応用が可能であり、幅広い応用を進めていきたいと考えています。」(和田辰也)詳しい研究内容について
研究者情報
研究者名
北澤 正清
書誌情報
【KURENAIアクセスURL】
http://hdl.handle.net/2433/293754
http://hdl.handle.net/2433/293754
【書誌情報】
Tatsuya Wada, Masakiyo Kitazawa, Kazuyuki Kanaya (2025). Locating Critical Points Using Ratios of Lee-Yang Zeros. Physical Review Letters, 134, 16, 162302.
Tatsuya Wada, Masakiyo Kitazawa, Kazuyuki Kanaya (2025). Locating Critical Points Using Ratios of Lee-Yang Zeros. Physical Review Letters, 134, 16, 162302.
関連部局





